この計算は,ここ,を参考にして,
\(\Large \begin{eqnarray} t_1 \cdot \alpha \cdot \displaystyle \sum_{ n = 0 }^{ \infty} (n+1)(1- \alpha)^n
&=&
t_1 \cdot \alpha \cdot \frac{1}{1-(1- \alpha)^2} \\
&=& \frac{t_1}{ \alpha} \\
&=& \frac{\frac{1}{k_B} + \frac{1}{k_A+k_C}}{\frac{k_A}{k_A+k_C}} \\
&=& \left(
\frac{1}{k_B} + \frac{1}{k_A+k_C} \right) \times \frac{k_A+k_C}{k_A} \\
&=& \frac{k_A + k_C}{ k_B k_C} + \frac{1}{k_C} \\
&=& \frac{ k_A + k_B +k_C}{k_B k_C} \\
\end{eqnarray} \)
となります.
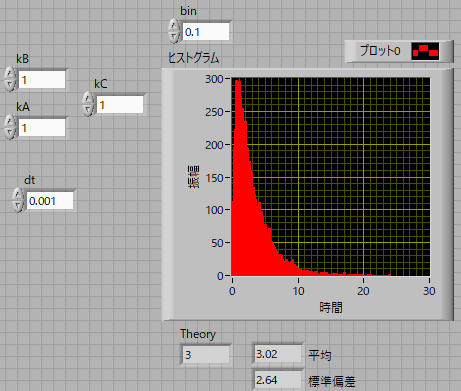
実際にモンテカルロシュミレーションにて確認してみると,

kB=1, kC=1, kA=1,のとき一致していることがわかります
図下の,Theoryが計算値,平均がシミュレーションによる平均値.

kB=2, kC=2, kA=1,のときにも一致していることがわかります